Interview of Associate Professor Yu KAWANO
Control Engineering Tailored to Nonlinear Dynamics, Enabling Design of Complex Phenomena

| Program | JST FOREST (Fusion Oriented REsearch for disruptive Science and Technology) Program | Researchers selected in the FY | 2022 |
|---|
Using Mathematical Formulas to Describe the Change in Phenomena over Time
My work focuses on controlling nonlinear dynamics, which has potential for application in a variety of fields. Control engineering came about during the Industrial Revolution, when it became necessary to automate machines; they sought to create the mechanisms using mathematics. Today, control engineering is integral to every industry we encounter in daily life, such as cars, robots, home appliances, and the internet. In recent years, control engineering has expanded beyond industry to applications in chemistry, biology, and economics. As it relates to dynamics—the phenomenon of change over time—control engineering uses differential equations and other formulae to express changes in dynamics in all areas, and seeks to manipulate them.
In contrast to conventional control engineering, which is the consideration of linear dynamics, which, on a 2D graph would show as straight lines, the control engineering I work on pertains to nonlinear dynamics. Nonlinear changes are more complex than linear changes, and are characterized by the fact that past events have a nontrivial effect on present and future events.
Examples of non-linear phenomena in nature include the generation of biological cells by genes and the synchronization of neuron networks in brain cells. And as society progresses toward self-driving vehicles, the collective movement of networked automobiles could also be described as nonlinear dynamics.
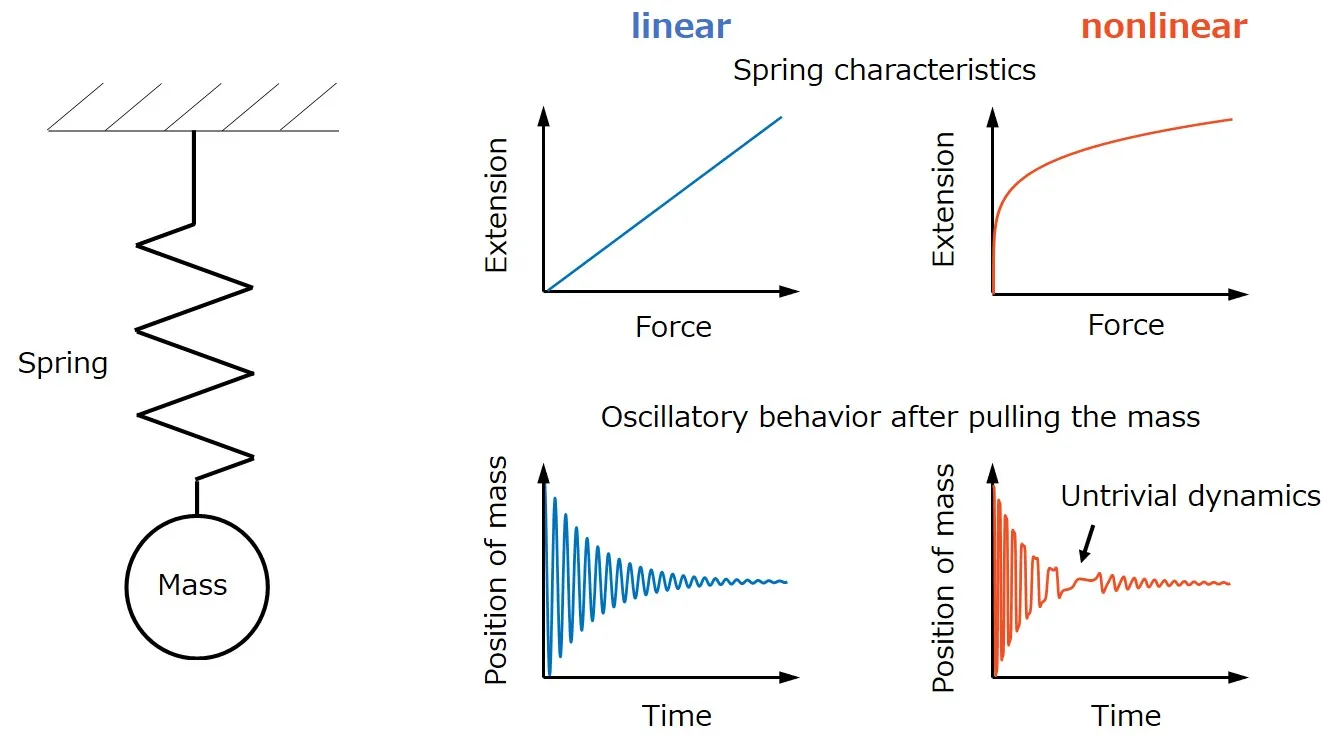
The dynamics of spring mass systems in the cases of linear and nonlinear springs.
Controlling such large-scale nonlinear networks requires mathematics far more complex than linear control engineering. The sheer volume of calculations required is drastically different and takes vast amounts of time even on a supercomputer.
Mathematical Models with Real-world Applications, e.g., Smart-Grid Power Generation Networks
The aim of my research, which was selected for the Japan Science and Technology Agency’s Fusion Oriented Research for Disruptive Science and Technology in 2022, is to devise a mathematical basis for controlling the diverse dynamics of large-scale nonlinear networks in a computationally feasible form. To that end, I am integrating three elements: contraction theory, the focus of much attention recently in the field of nonlinear system control; cone invariance, a property of dynamics; and dissipation theory, which is a combined analysis tool in system control.
I my research, I place great importance on the real-world applicability of the theories my team comes up with, and that’s why I have engaged in joint studies with researchers in various fields on application potential. One example of this is the control algorithm for distributed generation of next-generation power systems developed with researchers from the Faculty of Engineering at the University of Pavia in Italy and the Faculty of Science and Engineering at the University of Groningen in the Netherlands.
Conventional electric power systems use centralized generation, in which a large power plants generate and supply electricity to households and other users. This allows for centralized management, but it is susceptible to large-scale outages in major disasters like earthquakes. In contrast, the recent emergence of solar power generation, storage batteries, and electric vehicles has made it possible for users to generate and manage their own power, and the use of smart grids based on that system is attracting attention worldwide.
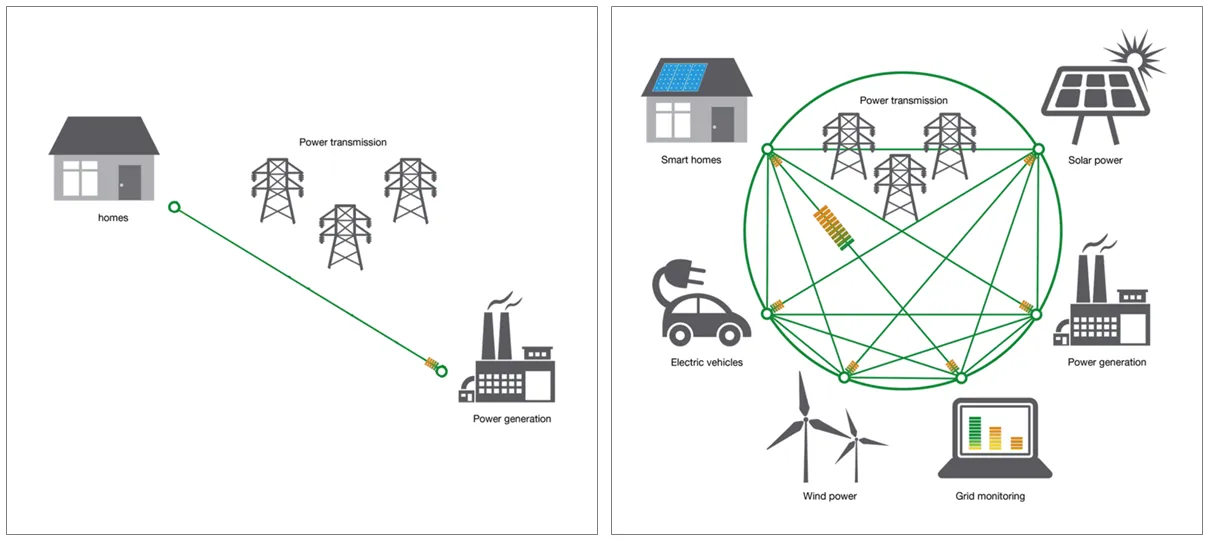
A conventional power generation system (left) and a smart grid envisaged for the future (right).
But establishing a smart grid requires an accurate forecast of the amount of electricity that each user can generate and the overall electricity demand as it changes from hour to hour, day and night. Obviously, more power-generating users participating in smart grids means less burden required of power plants, but the problem arises when the volume of data exceeds the ability to keep up with the calculations.
To solve this problem, we developed a control algorithm that allows autonomous, distributed power generation by users; it works by simply sharing the amount of power generated with other nearby users. The passivity of electric power systems has made it possible to control all power generation in a decentralized manner and reduce the amount of calculations.
A major feature of our control algorithm is that there is no need to tell the central power plant how much electricity each user is generating. For example, if energy consumption always increases at 20:00 at night in each household, we can assume that the residents are taking a bath. If there is no consumption over a certain period every day, we can assume that no one is home. But knowing when a home is empty raises issues in terms of crime prevention. In future, control engineering will need to construct algorithms that take such privacy issues into consideration, and that’s why I am working on a new algorithm—in parallel with my JST-supported research—that utilizes the idea of differential privacy.
Controlling electric power is just one possible application; the point is that nonlinear dynamics control theory can be used to abstract a broad range of problems in a computationally feasible form. I am determined to pursue my research with the aim of creating a future in which various phenomena in the world can be predicted and controlled through our research.
